Пропустить навигацию

Упражнения.

  1. Найти энтропию д.с.в. X, заданной распределением
    sfsf
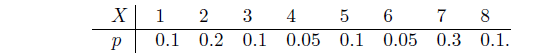
  2. Значения д. с. в. X1 и X2 определяются подбрасыванием двух идеальных монет, а д.с.в. Y равна сумме количества “гербов”, выпавших при подбрасывании этих монет. Сколько информации об X1 содержится в Y ?
  3. Сколько информации об X1 содержится в д.с.в. Z = (X1+1)2 − X2, где независимые д.с.в. X1 и X2 могут с равной вероятностью принимать значение либо 0, либо 1? Найти HX1 и HZ. Каков характер зависимости между X1 и Z?
  4. Д.с.в. X1, X2 — зависимы и распределены также как и соответствующие д.с.в. из предыдущей задачи. Найти I(X1,X2), если совместное распределение вероятностей X1 и X2 описывается законом
    sdfs
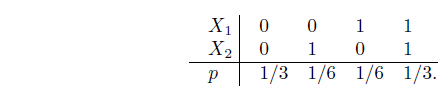
  5. Д. с. в. X1 и X2 определяются подбрасыванием двух идеальных тетраэдров, грани которых помечены числами от 1 до 4. Д. с. в. Y равна сумме чисел, выпавших при подбрасывании этих тетраэдров, т. е. Y = X1 + X2. Вычислить I(X1, Y ), HX1 и HY .
  6. Подсчитать сколько информации об X1 содержится в д.с.в. Z = X1 * X2, а также HZ. Д.с.в. X1 и X2 берутся из предыдущего упражнения.
  7. Д.с.в. X1 может принимать три значения −1, 0 и 1 с равными вероятностями. Д.с.в. X2 с равными вероятностями может принимать значения 0, 1 и 2. X1 и X2 — независимы. Y = X12 +X2. Найти I(X1, Y ), I(X2, Y ), HX1, HX2, HY.
  8. Найти энтропии д. с. в. X, Y , Z и количество информации, содержащейся в Z = X + Y относительно Y . X и Y — независимы и задаются распределениями
    ssf
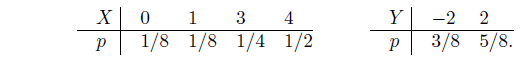
  9. Д.с.в. X равна количеству “гербов”, выпавших на двух идеальных монетках. Найти энтропию X. Придумать минимальный код для X, вычислить его среднюю длину и обосновать его минимальность.
  10. Д.с.в. X задана распределением P(X = 2n) = 1/2n, n = 1, 2, . . . Найти энтропию этой д.с.в. Придумать минимальный код для X, вычислить его среднюю длину и обосновать его минимальность.
  11. Про д.с.в. X известно, что ее значениями являются буквы кириллицы. Произведен ряд последовательных измерений X, результат которых — “ТЕОРИЯИНФОРМАЦИИ”. Составить на основании этого результата приблизительный закон распределения вероятностей этой д. с. в. и оценить минимальную среднюю длину кодов для X.