Полиномиальные коды
При полиномиальном кодировании каждое сообщение отождествляется с многочленом, а само кодирование состоит в умножении на фиксированный многочлен. Полиномиальные коды — блочные и отличаются от рассмотренных ранее только алгоритмами кодирования и декодирования.
Пусть a = a0 . . . am−1 — двоичное сообщение. Тогда сопоставим ему многочлен a(x) = a0 + a1x + · · · + am−1xm−1. Все вычисления происходят в поле классов вычетов по модулю 2, т. е. от результата любой арифметической операции берется остаток от его деления на 2.
Например, последовательности 10011 при m = 5 соответствует многочлен 1 + x3 + x4.
Зафиксируем некоторый многочлен степени k, g(x) = g0 + g1x + · · · + gkxk, g0 ≠ 0, gk ≠ 0.
Полиномиальный код с кодирующим многочленом g(x) кодирует слово сообщения a(x) многочленом b(x) = a(x)g(x) = b0 +b1x+· · ·+bn−1xn−1 или кодовым словом из коэффициентов этого многочлена b = b0 . . . bn−1.
Условия g0 ≠ 0 и gk ≠ 0 необходимы, потому что в противном случае b0 и bn−1 не будут нести никакой информации, т. к. они всегда будут нулями.
Пример. Рассмотрим кодирующий многочлен g(x) = 1 + x2 + x3. Сообщение 01011, отвечающее многочлену a(x) = x + x3 + x4, будет закодировано коэффициентами многочлена b(x) = g(x)a(x) = x+x5+x7, т.е. b = 01000101.
Полиномиальный код с кодирующим многочленом g(x) степени k является матричным кодом с кодирующей матрицей G размерности m×(m + k):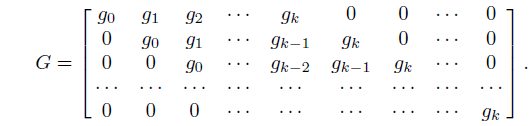
Т.е. ненулевые элементы в j-й строке — это последовательность коэффициентов кодирующего многочлена, расположенных с j-го по (j +k)-й столбцах.
Например, (3, 6)-код с кодирующим многочленом 1+x+x3 отвечает матрице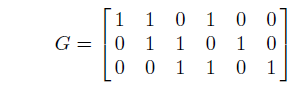
или отображению: 000 → 000000; 001 → 001101; 010 → 011010; 011 → 010111; 100 → 110100; 101 → 111001; 110 → 101110; 111 → 100011.
Полиномиальные коды являются групповыми.
Это следует из того, что коды, получаемые матричным кодированием, — групповые.
Рассмотрим (m, n)-код с кодирующим многочленом g(x). Строка ошибок e = e0 . . . en−1 останется необнаруженной в том и только в том случае, если соответствующий ей многочлен e(x) = e0 + e1x + · · · + en−1xn−1 делится на g(x).
Действительно, a(x)g(x) + e(x) делится на g(x) тогда и только тогда, когда e(x) делится на g(x). Поэтому любая ошибка, многочлен которой не делится на g(x), будет обнаружена и, соответственно, любая ошибка, многочлен которой делится на g(x), не может быть обнаружена.
Таким образом, обнаружение ошибки при использовании полиномиального кода с кодирующим многочленом g(x) может быть реализовано при помощи алгоритма деления многочленов с остатком: если остаток ненулевой, то при передаче произошло искажение данных.
Коды Хэмминга можно строить как полиномиальные, например, кодирующий многочлен x3 + x2 + 1 определяет совершенный (4, 7)-код, отличный от рассмотренного ранее.
Вообще же, если кодирующий многочлен g(x), порождающий соответствующий (m, n)-код, не является делителем ни одного из многочленов вида xj +1 при j < n, то минимальное расстояние между кодовыми словами порожденного им кода не меньше 3.
Пусть d — минимальное расстояние между кодовыми словами, оно равно минимуму среди весов ненулевых кодовых слов. Предположим d = 2. Тогда существует a(x) такой, что a(x)g(x) = b(x) и степень b(x) не больше n. Вес b равен 2, поэтому b(x) = xm + xl и l < m < n. Следовательно, b(x) = xl(xm−l + 1), что означает, что xm−l + 1 должен делиться на g(x), а это невозможно по условию. Если предположить, что d = 1, то это приведет к утверждению о том, что xm должен делиться на g(x), что тоже противоречит условию. Итак, d > 3.
Кодирующий многочлен x11 + x9 + x7 + x6 + x5 + x + 1 определяет совершенный (12, 23)-код Голея (Golay) с минимальным расстоянием между кодовыми словами 7.
В 1971 году финскими и советскими математиками было доказано, что кроме кодов Хэмминга и Голея других совершенных кодов нет.
Наиболее интересными среди полиномиальных кодов являются циклические коды, в которых вместе с любым кодовым словом вида b0 . . . bn−2bn−1 есть кодовое слово bn−1b0 . . . bn−2.
Понятие о кодах Боуза-Чоудхури-Хоккенгема
Остался открытым вопрос о методике построения кодов, минимальное расстояние между кодовыми словами которых равно заданному числу. В 1960 году независимо Боуз (Bose), Чоудхури (Chaudhuri) и Хоккенгем (Hocquengem) открыли способ построения полиномиальных кодов, удовлетворяющих таким требованиям. Эти коды получили названия кодов Боуза-Чоудхури-Хоккенгема или БЧХ-кодов (BCH codes).
БЧХ-коды могут быть не только двоичными, например, на практике достаточно широко используются недвоичные коды Рида-Соломона (Reed, Solomon), но далее будут рассматриваться только двоичные.
Многочлен g(x) степени k называется примитивным, если xj + 1 делится на g(x) без остатка для j = 2k − 1 и не делится ни для какого меньшего значения j.
Например, многочлен 1 + x2 + x3 примитивен: он делит x7 + 1, но не делит xj + 1 при j < 7. Примитивен также многочлен 1 + x3 + x4 — он делит x15 + 1, но не делит xj + 1 при j < 15.
Кодирующий многочлен g(x) для БЧХ-кода, длина кодовых слов которого n, строится так. Находится примитивный многочлен минимальной степени q такой, что n ≤ 2q − 1 или q ≥ log2(n + 1). Пусть α — корень этого многочлена, тогда рассмотрим кодирующий многочлен g(x) = НОК (m1(x), . . . ,md−1(x)), где m1(x), . . . ,md−1(x) — многочлены минимальной степени, имеющие корнями соответственно α, α2, . . . , αd−1.
Построенный кодирующий многочлен производит код с минимальным расстоянием между кодовыми словами, не меньшим d, и длиной кодовых слов n [1].
Пример. Нужно построить БЧХ-код с длиной кодовых слов n = 15 и минимальным расстоянием между кодовыми словами d = 5. Степень примитивного многочлена равна q = log2(n + 1) = 4 и сам он равен x4 + x3 + 1. Пусть α — его корень, тогда α2 и α4 — также его корни.
Минимальным многочленом для α3 будет x4 +x3 +x2 +x+1. Следовательно,
g(x) = НОК (x4 + x3 + 1, x4 + x3 + x2 + x + 1) = (x4 + x3 + 1)(x4 + x3 + x2 + x + 1) = x8 + x4 + x2 + x + 1.
Степень полученного многочлена равна 8, следовательно, построенный БЧХ-код будет (7, 15)-кодом. Слово 1000100 или a(x) = x4 + 1 будет закодировано кодовым словом a(x)g(x) = x12 + x6 + x5 + x2 + x + 1 или 111001100000100.
Можно построить [1] двоичный БЧХ-код с кодовыми словами длины n = 2q − 1 и нечетным минимальным расстоянием d, у которого число контрольных символов не больше ![]()
Первый БЧХ-код, примененный на практике, был (92, 127)-кодом, исправляющим ошибки кратности до 5, но наиболее широкое распространение получил (231, 255)-код, обнаруживающий ошибки кратности до 6.
БЧХ-коды умеренной длины не слишком далеки от совершенных или квазисовершенных кодов. Коды Хэмминга, например, являются БЧХ-кодами, а БЧХ-коды с минимальным весом кодового слова 5 — квазисовершенны. Но с ростом длины кодовых слов качество БЧХ-кодов падает. Код Голея, например, — это не код БЧХ.
Циклические избыточные коды
Циклический избыточный код (Cyclical Redundancy Check—CRC) имеет фиксированную длину и используется для обнаружения ошибок.
Наибольшее распространения получили коды CRC-16 и CRC-32, имеющие длину 16 и 32 бита соответственно. Код CRC строится по исходному сообщению произвольной длины, т.е. этот код не является блочным в строгом смысле этого слова. Но при каждом конкретном применении этот код — блочный, (m, m + 16)-код для CRC-16 или (m, m + 32)-код для CRC-32.
Вычисление значения кода CRC происходит посредством деления многочлена, соответствующего исходному сообщению (полином-сообщение), на фиксированный многочлен (полином-генератор). Остаток от такого деления и есть код CRC, соответствующий исходному сообщению. Для кода CRC-16 полином-генератор имеет степень 16, а для CRC-32 — 32. Полиномы-генераторы подбираются специальным образом и для кодов CRC-16/32 стандартизированы Международным консультативным комитетом по телеграфной и телефонной связи (CCITT). Для CRC-16, например, стандартным является полином-генератор x16 + x12 + x5 + 1.
Пример построения CRC-4 кода для сообщения 11010111, используя полином-генератор x4+x3+x2+1. Исходному сообщению соответствует полином x7+x6+x4+x2+x+1, т.е. нумерация битов здесь начинается справа.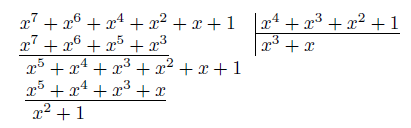
Полиному x2 + 1 соответствуют биты 0101 — это и есть CRC-4 код.
Существуют быстрые алгоритмы для расчета CRC-кодов, использующие специальные таблицы, а не деление многочленов с остатком.
CRC-коды способны обнаруживать одиночную ошибку в любой позиции и, кроме того, многочисленные комбинации кратных ошибок, расположенных близко друг от друга. При реальной передаче или хранении информации ошибки обычно группируются на некотором участке, а не распределяются равномерно по всей длине данных. Таким образом, хотя для идеального случая двоичного симметричного канала CRC-коды не имеют никаких теоретических преимуществ по сравнению, например, с простыми контрольными суммами, для реальных систем эти коды являются очень полезными.
Коды CRC используются очень широко: модемами, телекоммуникационными программами, программами архивации и проверки целостности данных и многими другими программными и аппаратными компонентами вычислительных систем.