Метод Шеннона-Фэно состоит в следующем, значения д.с.в. располагают в порядке убывания их вероятностей, а затем последовательно делят на две части с приблизительно равными вероятностями, к коду первой части добавляют 0, а к коду второй — 1.
Для предшествующего примера получим:
| X→ | p | code(X→) |
| 00 | 9/16 | 0 |
| 01 | 3/16 | 10 |
| 10 | 3/16 | 110 |
| 11 | 1/16 | 111 |
ML1(X→) = 27/32 = 0.84375 бит/сим.
Еще один пример. Код составляется после сортировки, т. е. после перестановки значений B и C.
| X | p | code(X) |
| A | 0.4 | 0 |
| B | 0.2 | 11 |
| C | 0.4 | 10 |
ML(X) = ML1(X) = 1.6 бит/сим,
HX = log25 − 0.8 ≈ 1.523 бит/сим.
Метод Хаффмена (Huffman) разработан в 1952 г. Он более Метод Хаффмена (Huffman) разработан в 1952 г. Он более практичен и никогда по степени сжатия не уступает методу Шеннона-Фэно, более того, он сжимает максимально плотно. Код строится при помощи двоичного (бинарного) дерева. Вероятности значений д.с.в. приписываются его листьям; все дерево строится, опираясь на листья. Величина, приписанная к узлу дерева, называется весом узла. Два листа с наименьшими весами создают родительский узел с весом, равным сумме их весов; в дальнейшем этот узел учитывается наравне с оставшимися листьями, а образовавшие его узлы от такого рассмотрения устраняются. После постройки корня нужно приписать каждой из ветвей, исходящих из родительских узлов, значения 0 или 1. Код каждого значения д.с.в. — это число, получаемое при обходе ветвей от корня к листу, соответствующему данному значению.
Для методов Хаффмена и Шеннона-Фэно каждый раз вместе с собственно сообщением нужно передавать и таблицу кодов. Например, для случая из примера 2 нужно сообщить, что коду 10 соответствует символ C, коду 0 — A и т.д.
Построим коды Хаффмена для значений д.с.в. из двух предыдущих примеров.
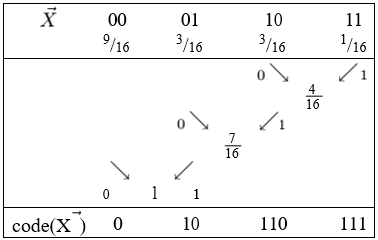
ML1(X→) = ML(X→)/2 = 27/32 = 0.84375 бит/сим.
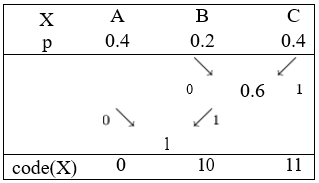
ML1(X) = ML(X) = 1.6 бит/сим.