Матричное кодирование
Ранее каждая схема кодирования описывалась таблицами, задающими кодовое слово длины n для каждого исходного слова длины m.
Для блоков большой длины этот способ требует большого объема памяти и поэтому непрактичен. Например, для (16, 33)-кода потребуется 33 * 216 = 2 162 688 бит.
Гораздо меньшего объема памяти требует матричное кодирование. Пусть E матрица размерности m×n, состоящая из элементов eij , где i — это номер строки, а j — номер столбца. Каждый из элементов матрицы eij может быть либо 0, либо 1. Кодирование реализуется операцией b = aE или bj = a1e1j + a2e2j + · · · + amemj, где кодовые слова
рассматриваются как векторы, т.е как матрицы-строки размера 1 × n.
Пример. Рассмотрим следующую 3 × 6-матрицу:
Тогда кодирование задается такими отображениями: 000 → 000000, 001 → 001111, 010 → 010011, 011 → 011100, 100 → 100110, 101 → 101001, 110 → 110101, 111 → 111010.
Рассмотренный пример показывает преимущества матричного кодирования: достаточно запомнить m кодовых слов вместо 2m слов. Это общий факт.
Кодирование не должно приписывать одно и то же кодовое слово разным исходным сообщениям. Простой способ добиться этого состоит в том, чтобы m столбцов (в предыдущем примере — первых) матрицы E образовывали единичную матрицу. При умножении любого вектора на единичную матрицу получается этот же самый вектор, следовательно, разным векторам-сообщениям будут соответствовать разные вектора систематического кода.
Матричные коды называют также линейными кодами. Для линейных (n−r, n)-кодов с минимальным расстоянием Хэмминга d существует нижняя граница Плоткина (Plotkin) для минимального количества контрольных разрядов r при n ≥ 2d − 1, r ≥ 2d − 2 − log2d.
Групповые коды
Множество всех двоичных слов a = a1 . . . am длины m образует абелеву (коммутативную) группу относительно поразрядного сложения.
Пусть E — кодирующая m × n-матрица, у которой есть m × m-подматрица с отличным от нуля определителем, например, единичная. Тогда отображение a ! aE переводит группу всех двоичных слов длины m в группу кодовых слов длины n.
Предположим, что a = a1 . . . am = a'+a''. Тогда для b = b1 · · · bn = aE, b' = a'E, b'' = a''E, получаем: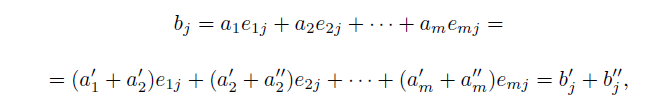
Следовательно, взаимно-однозначное отображение группы двоичных слов длины m при помощи заданной матрицы E сохраняет свойства групповой операции, что означает, что кодовые слова образуют группу.
Блочный код называется групповым, если его кодовые слова образуют группу. Если код является групповым, то наименьшее расстояние между
двумя кодовыми словами равно наименьшему весу ненулевого слова.
Это следует из соотношения d(bi, bj) = w(bi + bj). В предыдущем примере наименьший вес ненулевого слова равен 3. Следовательно, этот код способен исправлять однократную ошибку или обнаруживать однократную и двойную.
При использовании группового кода незамеченными остаются те и только те ошибки, которые отвечают строкам ошибок, в точности равным кодовым словам.
Такие строки ошибок переводят одно кодовое слово в другое. Следовательно, вероятность того, что ошибка останется необнаруженной, равна сумме вероятностей всех строк ошибок, равных кодовым словам.
В рассмотренном примере вероятность ошибки равна 4p3q3+3p2q4. Рассмотрим задачу оптимизации декодирования группового кода с двоичной матрицей кодирования E. Требуется минимизировать вероятность того, что D(T(aE)) ≠ a.
Схема декодирования состоит из группы G всех слов, которые могут быть приняты (#G = 2n). Так как кодовые слова B образуют нормальную (нормальность следует из коммутативности G) подгруппу G, то множеству G можно придать структуру таблицы: будем записывать в одну строку те элементы G, которые являются членами одного смежного класса G по B. Первая строка, соответствующая нулевому слову из G, будет тогда всеми кодовыми словами из B, т. е. b0, b1, . . . , b2m-1.
В общем случае, если gi ∈ G, то строка, содержащая gi (смежный класс giB) имеет вид b0 + gi, b1 + gi, . . . , b2m-1 + gi.
Лидером каждого из таких построенных смежных классов называется слово минимального веса.
Каждый элемент g из G однозначно представляется в виде суммы gi + bj , где gj ∈ G — лидер соответствующего смежного класса и bj ∈ B.
Множество классов смежности группы образуют фактор-группу, которая есть фактор-множество множества G по отношению эквивалентности-принадлежности к одному смежному классу, а это означает, что множества, составляющие это фактор-множество, образуют разбиение G. Отсюда следует, что строки построенной таблицы попарно либо не пересекаются, либо совпадают.
Если в рассматриваемой таблице в первом столбце записать лидеры, то полученная таблица называется таблицей декодирования. Она имеет вид: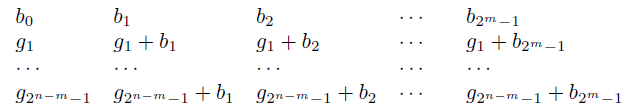
То, что строк будет 2n-m следует из теоремы Лагранжа, т.к. 2n-m — это порядок фактор-группы G/B, #(G/B) = #(G)/#(B), #B = 2m.
Декодирование слова g = bj +gi состоит в выборе кодового слова bj в качестве переданного и последующем применении операции, обратной умножению на E. Такая схема декодирования сможет исправлять ошибки.
Для (3, 6)-кода из рассматриваемого примера таблица декодирования будет следующей:
000000 100110 010011 110101 001111 101001 011100 111010
100000 000110 110011 010101 101111 001001 111100 011010
010000 110110 000011 100101 011111 011001 001100 101010
001000 101110 011011 111101 000111 100001 010100 110010
000100 100010 010111 110001 001011 101101 011000 111110
000010 100100 010001 110111 001101 101011 011110 111000
000001 100111 010010 110100 001110 101000 011101 111011
000101 100011 010110 110000 001010 101100 011001 111111.
Первая строка в ней — это строка кодовых слов, а первый столбец — это лидеры.
Чтобы декодировать слово bj + e, следует отыскать его в таблице и выбрать в качестве переданного слово в том же столбце и в первой строке.
Например, если принято слово 110011 (2-я строка, 3-й столбец таблицы), то считается, что было передано слово 010011; аналогично, если принято слово 100101 (3-я строка, 4-й столбец таблицы), переданным считается слово 110101, и т.д.
Групповое кодирование со схемой декодирования посредством лидеров исправляет все ошибки, строки которых совпадают с лидерами.
Следовательно, вероятность правильного декодирования переданного по двоичному симметричному каналу кода равна сумме вероятностей всех лидеров, включая нулевой.
В рассмотренной схеме вероятность правильной передачи слова будет p6+ 6p5q + p4q2.
Кодовое слово любого столбца таблицы декодирования является ближайшим кодовым словом ко всем прочим словам данного столбца.
Пусть переданное слово bi принято как bi + e, d(bi, bi + e) = ω(e), т. е. это расстояние равно весу соответствующего лидера. Расстояние от bi + e до любого другого кодового слова bj равно весу их поразрядной суммы, т.е. d(bj , bi + e) = ω(bj + bi + e) = d(bj + bi, e) = d(bk, e) = ω(bk + e) > ω(e), т. к. e — лидер смежного класса, к которому принадлежат как bk + e, так и bi + e.
Доказано, при схеме декодирования лидерами по полученному слову берется ближайшее к нему кодовое.