Лекция 3. Вероятностный подход к измерению дискретной информации. Понятие "энтропия" и "количество информации".

Вероятностный подход к измерению дискретной и непрерывной информации

В основе теории информации лежит предложенный Шенноном способ измерения количества информации, содержащейся в одной сл.в. относительно другой сл. в. Этот способ приводит к выражению количества информации числом.

Для д.с.в. X и Y , заданных законами распределения P(X = X_i) = p_i, P(Y = Y_j) = q_j и совместным распределением P(X = X_i, Y = Y_j) = p_ij , количество информации, содержащейся в X относительно Y , равно 

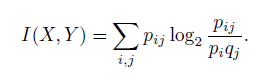
Для непрерывных сл. в. X и Y , заданных плотностями распределения вероятностей pX(t₁), pY (t₂) и p_XY (t₁, t₂), аналогичная формула имеет вид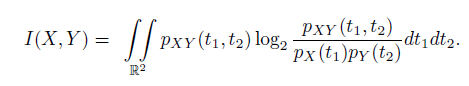

Очевидно, что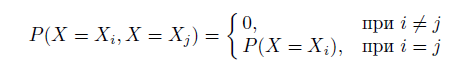

и, следовательно,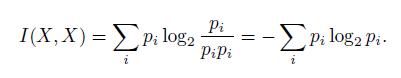

Энтропия д.с.в. X в теории информации определяется формулой 

H(X) = HX = I(X,X).

1) Логарифмированием из очевидного для всех x неравенства e^x−1 > x (равенство устанавливается только при x = 1) получается неравенство x−1 ≥ ln x или (x−1)/ln 2 ≥ log₂x.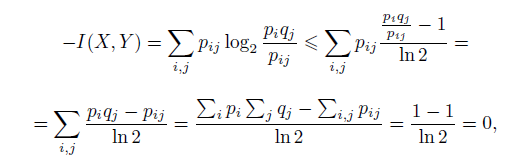

т.е. I(X, Y ) = 0 только при p_ij = p_iq_j для всех i и j, т.е. при независимости X и Y . Если X и Y независимы, то p_ij = p_iq_j и, следовательно, аргументы логарифмов равны 1 и, следовательно, сами логарифмы равны 0, что означает, что I(X, Y ) = 0;
2) Следует из симметричности формул относительно аргументов;
3) Если HX = 0, то все члены суммы, определяющей HX, должны быть нули, что возможно тогда и только тогда, когда X — константа;
4) Из четырех очевидных соотношений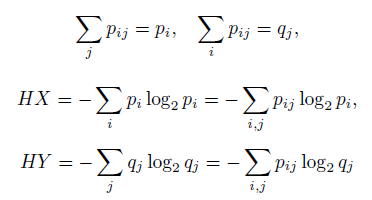

получается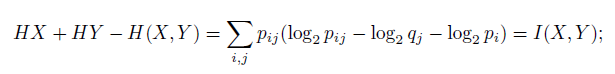

5) Нужно доказать I(X, Y ) = HX + HY − H(X, Y ) ≤ HX или HY − H(X, Y ) ≤ 0.

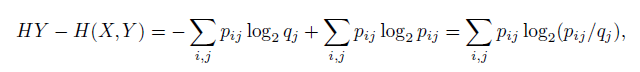
но p_ij = P(X = X_i, Y = Y_j) ≤ q_j = P(Y = Y_j), а значит аргументы у всех логарифмов не больше 1 и, следовательно, значения логарифмов не больше 0, а это и значит, что вся сумма не больше 0.

Если HX = I(X, X) = I(X, Y ), то для каждого i p_ij равно либо q_j , либо 0. Но из p_ij = P(X = X_i, Y = Y_j) = P(X = X_i/Y = Y_j)P(Y = Y_j) ∈ {q_j , 0} следует P(X = X_i/Y = Y_j) ∈ {0, 1}, что возможно только в случае,
когда X — функция от Y .

При независимости сл. в. X и Y одна из них ничем не описывает другую, что и отражается в том, что для таких сл.в. I(X, Y ) = 0.

Рассмотрим пример измерения количества информации при подбрасывании двух игральных костей.
Пусть заданы д. с. в. X₁, X₂ и Y . X₁ и X₂ — количества очков, выпавших соответственно на 1-й и 2-й игральной кости, а Y = X₁ + X₂.
Найти I(Y, X₁), I(X₁, X₁), I(Y, Y ).
Законы распределения вероятностей для д.с.в. X1 и X2 совпадают, т.к. кости одинаковые и без изъянов.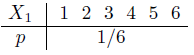
, т.е. при j = 1...6 q_j = P(X₁ = j) = 1/6.
Закон распределения вероятностей для д.с.в. Y,

P(Y = i) = P(X₁ + X₂ = i), i = 2...12,
вследствие того, что X₁, X₂ — независимы и поэтому P(X₁ = n, X₂ = m) = P(X₁ = n) P(X₂ = m),
будет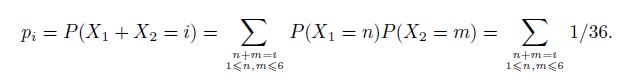

Таблицы, определяющие Y: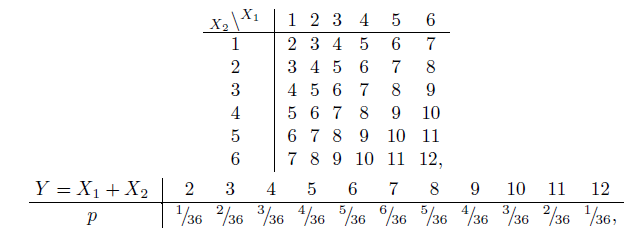

т.е. при i = 2...12, p_i = P(Y = i) = (6 − |7 − i|)/36.

Закон совместного распределения вероятностей д.с.в. X1 и Y будет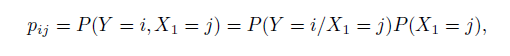

например,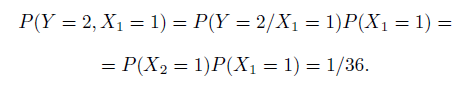

В общем случае получится

Тогда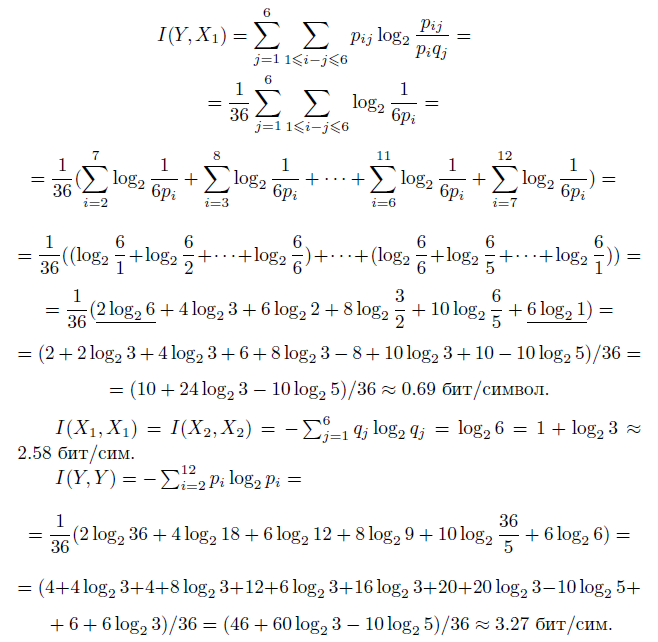

Здесь 0 < I(Y, X₁) = I(Y, X₂) < I(X₁, X₁) = I(X₂, X₂) < I(Y, Y ), что соответствует свойствам информации.
Подчеркнутый член 1/36 2log₂6 = I(X₁, X₁)/18 в расчете I(X₁, Y ) соответствует информации о двух случаях из 36, когда Y = 2 и Y = 12, которые однозначно определяют X₁. Шесть случаев, когда Y = 7, не несут никакой информации об X₁, что соответствует подчеркнутому члену 6log₂1 = 0.

Расчеты можно проводить, используя 4-е свойство информации, через энтропию.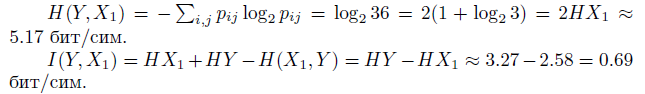

Расчет количества информации с использованием 4-го свойства, а не определения, обычно требует меньше вычислений.

Рассмотрим более простой пример. Пусть д. с.в. X равна количеству очков, выпавших на игральной кости, а д. с. в. Y равна 0, если выпавшее количество очков нечетно, и 1, если выпавшее количество очков четно. Найти I(X, Y ) и I(Y, Y ).

Составим законы распределения вероятностей д.с.в. X и Y .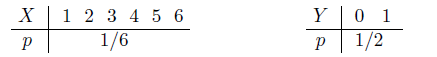

Таким образом, при i = 1...6 p_i = P(X = i) = 1/6 и, соответственно, при j = 0...1 q_j = P(Y = j) = 1/2.

Составим также закон совместного распределения вероятностей этих д.с.в.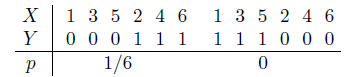

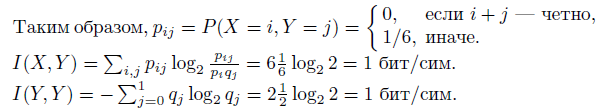
Точное количество выпавших очков дает точную информацию о четности, т.е. 1 бит. Из I(X, Y ) = I(Y, Y ) = 1 бит/сим и 3-го свойства информации следует, что информация об X полностью определяет Y , но не наоборот, т.к. I(X, Y ) ≠ I(X, X) = 1+log₂3 ≈ 2.58 бит/сим. Действительно, Y функционально зависит от X, а X от Y функционально не зависит.

Расчеты через энтропию будут следующими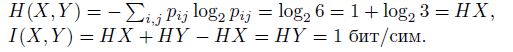

Смысл энтропии Шеннона
Энтропия д.с.в. — это минимум среднего количества бит, которое нужно передавать по каналу связи о текущем значении данной д.с.в.

Рассмотрим пример (скачки). В заезде участвуют 4 лошади с равными шансами на победу, т.е. вероятность победы каждой лошади равна 1/4. Введем д. с. в. X, равную номеру победившей лошади. Здесь HX = 2. После каждого заезда по каналам связи достаточно будет передавать два бита информации о номере победившей лошади. Кодируем номер лошади следующим образом: 1—00, 2—01, 3—10, 4—11. Если ввести функцию L(X), которая возвращает длину сообщения, кодирующего заданное значение X, то м. о. ML(X) — это средняя длина сообщения, кодирующего X. Можно формально определить L через две функции L(X) = len(code(X)), где code(X) каждому значению X ставит в соответствие некоторый битовый код, причем, взаимно однозначно, а len возвращает длину в битах для любого конкретного кода.

В этом примере ML(X) = HX.
Пусть теперь д.с.в. X имеет следующее распределение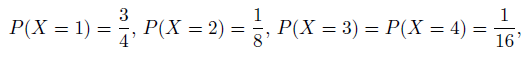

т.е. лошадь с номером 1 — это фаворит. Тогда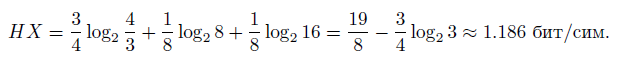

Закодируем номера лошадей: 1—0, 2—10, 3—110, 4—111, — т. е. так, чтобы каждой код не был префиксом другого кода (подобное кодирование называют префиксным). В среднем в 16 заездах 1-я лошадь должна победить в 12 из них, 2-я — в 2-х, 3-я — в 1-м и 4-я — в 1-м. Таким образом, средняя длина сообщения о победителе равна (1 * 12 + 2 * 2 + 3 * 1 + 3 * 1)/16 = 1.375 бит/сим или м. о. L(X). Действительно, L(X) сейчас задается следующим распределением вероятностей: P(L(X) = 1) = 3/4,  P(L(X) = 2) = 1/8,   P(L(X) = 3) = 1/8.
Следовательно,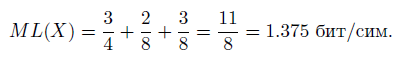

Итак, ML(X) > HX.

Можно доказать, что более эффективного кодирования для двух рассмотренных случаев не существует.
То, что энтропия Шеннона соответствует интуитивному представлению о мере информации, может быть продемонстрировано в опыте по определению среднего времени психических реакций. Опыт заключается в том, что перед испытуемым человеком зажигается одна из N лампочек, которую он должен указать. Проводится большая серия испытаний, в которых каждая лампочка зажигается с определенной вероятностью , где i — это номер лампочки. Оказывается, среднее время, необходимое для правильного ответа испытуемого, пропорционально величине энтропии − , а не числу лампочек N, как можно было бы подумать. В этом опыте предполагается, что чем больше информации будет получено человеком, тем дольше будет время ее обработки и, соответственно, реакции на нее.