Раздел 3. Задачи выбора решений, отношения, функции выбора, функции полезности, критерии
3.3 Функция полезности
Пусть заданы критерии 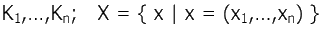 - множество векторных оценок вариантов по этим критериям.
Пусть на X задано R - отношение предпочтения. Числовая функция
- множество векторных оценок вариантов по этим критериям.
Пусть на X задано R - отношение предпочтения. Числовая функция  называется функцией полезности (ценности, предпочтительности), если она обладает следующим свойством:
называется функцией полезности (ценности, предпочтительности), если она обладает следующим свойством: 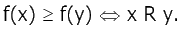
Если известна функция полезности, то поиск оптимального варианта сводится к задаче нахождения  , - аргумента максимума функции полезности на множестве X.
, - аргумента максимума функции полезности на множестве X.
Как найти функцию полезности? Методы построения функции полезности делятся на эвристические и аксиоматические.
К эвристическим методам можно отнести метод главного критерия и метод обобщенного критерия.
Метод главного критерия сводится к оптимизации по одному выбранному критерию, при условии, что остальные критерии не больше (или не меньше) приемлемых значений.
Метод обобщенного критерия заключается в свeртке набора критериев в числовую функцию, которая и будет являться функцией полезности.
Виды свeрток:
1) аддитивная свeртка:
2) мультипликативнаясвeртка: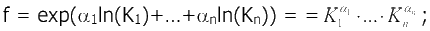
3) приведенная свѐртка:  по всем
по всем  (или
(или  по всем
по всем  ).
).
Аксиоматические методы построения функции полезности - это формальные методы, основанные на том, что формулируются специальные предположения (аксиомы) о свойствах предпочтения, выполнение которых гарантирует существование функции полезности конкретного вида.
Обычно, при использовании таких методов функцию полезности строят в аддитивном виде:

как сумму функций полезности по каждому критерию с некоторыми весовыми коэффициентами 
Пусть  - подмножество множества критериев , т.е.
группа критериев с номерами из множества
- подмножество множества критериев , т.е.
группа критериев с номерами из множества  .
Тогда
.
Тогда  - все остальные критерии ,
а векторная оценка х представляется в виде
- все остальные критерии ,
а векторная оценка х представляется в виде 
Говорят, что критерии  не зависят по предпочтению от критериев
не зависят по предпочтению от критериев  ,
если предпочтения для любых двух оценок
,
если предпочтения для любых двух оценок 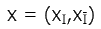 и
и  содержащих одинаковые компоненты с номерами из
содержащих одинаковые компоненты с номерами из 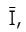 не зависят от самих значений этих компонент.
не зависят от самих значений этих компонент.
Пример 1.
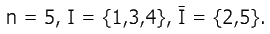
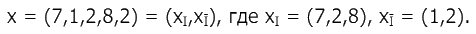

Таким образом, 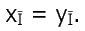
Если критерии  не зависят по предпочтению от критериев
не зависят по предпочтению от критериев  и оценка х предпочтительнее, чем оценка у, то и,
например, оценка
и оценка х предпочтительнее, чем оценка у, то и,
например, оценка 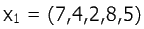 будет предпочтительнее, чем
будет предпочтительнее, чем  , потому что их значения по критерия м из группы
, потому что их значения по критерия м из группы  совпадают с соответствующими значениями
оценок х и у, а оценки по остальным критериям одинаковые. Таким образом, вместо
совпадают с соответствующими значениями
оценок х и у, а оценки по остальным критериям одинаковые. Таким образом, вместо 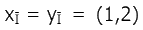 можно подставить любую оценку (а, b) и предпочтение сохранится: (7,а,2,8,b) предпочтительнее, чем (4,а,8,3,b).
можно подставить любую оценку (а, b) и предпочтение сохранится: (7,а,2,8,b) предпочтительнее, чем (4,а,8,3,b).
Критерии 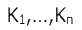 такие, что любой набор
такие, что любой набор  из них не зависит по предпочтению от остальных критериев
из них не зависит по предпочтению от остальных критериев  , называются взаимно независимыми по предпочтению.
, называются взаимно независимыми по предпочтению.
Теорема Дебре (критерий существования аддитивной функции полезности): функция полезности может быть задана в аддитивном виде (*) тогда и только тогда, когда критерии 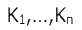 взаимно независимы по предпочтению (при
взаимно независимы по предпочтению (при 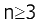 ).
).
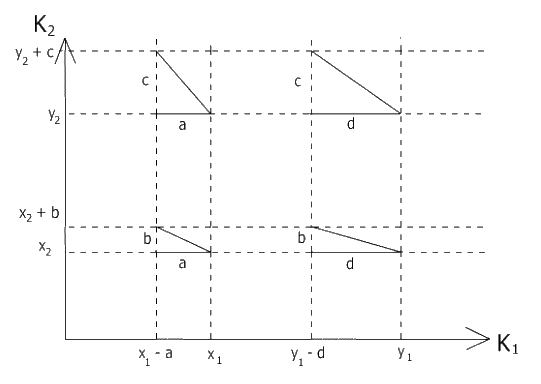
При n=2, кроме взаимной независимости критериев, требуется выполнение условия соответственных замещений (при 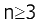 оно выполняется автоматически):
оно выполняется автоматически):
 если
если 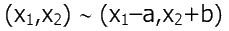 и
и  то
то
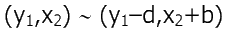 и
и 
Т.е., если увеличение на b и c разных значений  и
и  критерия
критерия 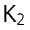 при
некотором опорном значении
при
некотором опорном значении  критерия
критерия  компенсируется одним и тем же
уменьшением этого значения
компенсируется одним и тем же
уменьшением этого значения  критерия
критерия  , то такие же увеличения b и c тех же
значений
, то такие же увеличения b и c тех же
значений  и
и  критерия
критерия 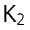 сохраняются и при любом другом опорном значении
сохраняются и при любом другом опорном значении
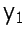 критерия
критерия  .
.
Как осуществляется проверка взаимной независимости критериев по предпочтению?
Непосредственно по определению проверить независимость критериев затруднительно, т.к. даже при небольших n возникает большое число вариантов, которые надо проверить.
Утверждение (Леонтьева-Гормана): если любая пара критериев  не зависит по предпочтению от остальных (n-2) критериев, то все критерии
не зависит по предпочтению от остальных (n-2) критериев, то все критерии 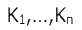 взаимно независимы по предпочтению.
взаимно независимы по предпочтению.
Таким образом, проверка сводится к установлению независимости только всех пар критериев от всех остальных критериев.
Пусть необходимо проверить на независимость по предпочтению наборы  и
и
 . Берѐм набор
. Берѐм набор 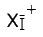 наилучших (явно хороших) значений и
подбираем (запрашиваем у ЛРП ) два разных набора
наилучших (явно хороших) значений и
подбираем (запрашиваем у ЛРП ) два разных набора  и
и
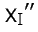 таких, что
таких, что 
Затем берѐм набор  самых плохих оценок и спрашиваем у ЛРП , сохранилось ли безразличие
самых плохих оценок и спрашиваем у ЛРП , сохранилось ли безразличие
 ? Если нет, то критерии
? Если нет, то критерии  зависят от критериев
зависят от критериев  .
Если да, повторяем процедуру еще для некоторых других
.
Если да, повторяем процедуру еще для некоторых других  и
и 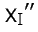 . Если всё время
безразличие остаётся, задаём вопрос в общем виде (сохранится ли безразличие
при любых наборах). Если да, то наборы критериев
. Если всё время
безразличие остаётся, задаём вопрос в общем виде (сохранится ли безразличие
при любых наборах). Если да, то наборы критериев  и
и  независимы.
независимы.