Раздел 6. Задачи скалярной оптимизации, линейные, нелинейные, дискретные
6.4 Симплекс метод
Решение любой задачи линейного программирования можно найти симплексным методом. Прежде чем применять указанный метод, следует записать исходную задачу в форме основной задачи линейного программирования, если она не имеет такой формы записи.
Общая математическая формулировка основной задачи линейного программирования: дана система m линейных уравнений с n неизвестными

и линейная функция Z=C1X1+C2X2+...+CnXn (2).
Требуется найти такое неотрицательное решение системы (1), при котором функция принимает наименьшее значение.
Если требуется найти наибольшее значение, то достаточно рассмотреть целевую функцию с противоположным знаком. Знак неравенства всегда можно заменить знаком равенства. Знак неравенства всегда можно заменить знаком равенства.
Например, х1-2х2≤6.
Введем неотрицательную переменную х3:
х1-2х2+х3=6. (задача решается и дополнительно введенные переменные в окончательном ответе игнорируются).
Симплекс-подход к решению задачи линейного программирования.
Преобразуем систему ограничений (1) так, чтобы какие-либо r ее неизвестных были выражены через остальные:
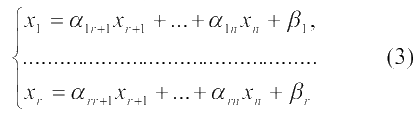
Переменные X1, …, Xr называются базисными, остальные переменные называются свободными. Совокупность базисных переменных называется базисом.
Подставляя вместо базисных переменных их выражения через свободные, мы можем целевую функцию представить через свободные неизвестные: 
Теперь, полагая, что все свободные переменные равны 0, из (3) получаем значения
базисных переменных:
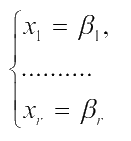
Таким образом получаем одно из решений системы (3), которое называется допустимым. Для этого решения значение целевой функции равно 
Основная идея симплекс-метода заключается в том, что последовательно переходят отодного базиса к другому так, чтобы новое значение целевой функции уменьшилось. Такимпутем в конечном итоге можно прийти к базису, дающему минимальное значение функции Z или выяснить, что задача не имеет решения. Переход от одного базиса кдругому происходит за счет удаления одной переменной из базиса и добавления в негодругой переменной. Вычисления по симплекс-методу осуществляют с помощью симплекс-таблиц. Для удобства будем считать, что система ограничений записана в виде:
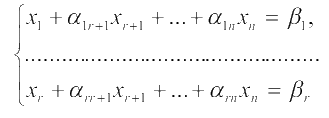
и целевая функция определена равенством: 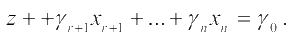
По исходным данным заполняется следующая таблица:

- Выяснить, есть ли в последней строке таблицы положительные числа (Y0 во внимание не принимается). Если все числа отрицательные, то процесс закончен. Базисное решение (β1, βr, 0, …, 0) является оптимальным. Соответствующее значение целевой функции Z = Y0 . Если в последней строке имеются положительные числа, перейти к п. 2.
- Рассмотреть столбец, соответствующий положительному числу из последней строки и выяснить, имеются ли в нем положительные числа. Если ни в одном из таких столбцов нет положительных чисел, то уменьшать значение целевой функции можно бесконечно и оптимального решения задачи не существует. Если найдется столбец, содержащий хотя бы один положительный элемент (если таких столбцов несколько, выбираем произвольный из них), отметить этот столбец вертикальной стрелкой и перейти к п. 3.
- Разделить свободные члены на соответствующие положительные числа из выделенного столбца и выбрать наименьшее частное. Отметить строку таблицы, соответствующую наименьшему частному горизонтальной стрелкой. Выделить разрешающий элемент aij, стоящий на пересечении отмеченных строки и столбца и перейти к п. 4.
- Разделить элементы выделенной строки исходной таблицы на разрешающий элемент. На месте разрешающего элемента появится 1. Полученная таким образом новая строка пишется на месте прежней в новой таблице (причем из базисных переменных исключается xi и на его месте записывается переменная xj). Перейти к п. 5.
- Каждая следующая строка новой таблицы образуется сложением соответствующей строки исходной таблицы и строки, записанной в п. 4, которая предварительно умножается на такое число, чтобы в клетках выделенного столбца появились нули. На этом заполнение новой таблицы заканчивается и происходит переход к п. 1.
Пример 1. Решить симплекс-методом задачу:
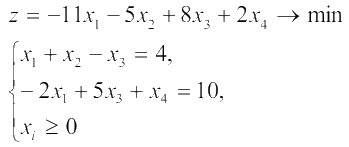
Решение:
Заполним исходную симплекс-таблицу:
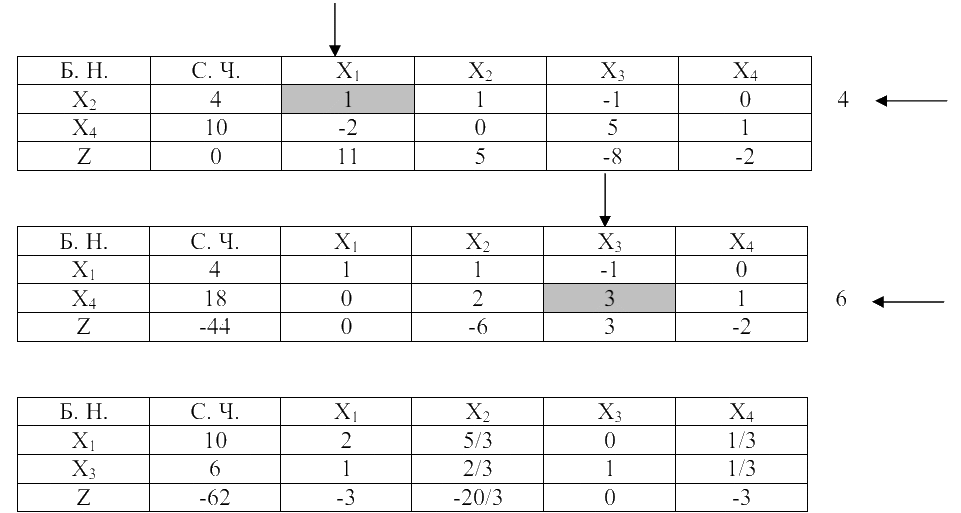
Оптимальное решение z = -62. Достигается при (10, 0, 6, 0).
Пример 2. Решить симплекс-методом задачу:
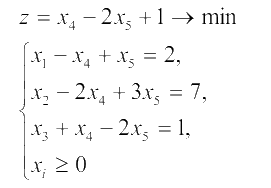

Оптимального решения нет.
Пример 2.
Пусть предприятием выпускается продукция четырех видов П1-П4 с использованием для этого ресурсов, виды и нормы расхода по которым, а также уровень получаемой от их реализации прибыли приведены в таблице. Необходимо получить вариант оптимального производства по критерию максимума прибыли.
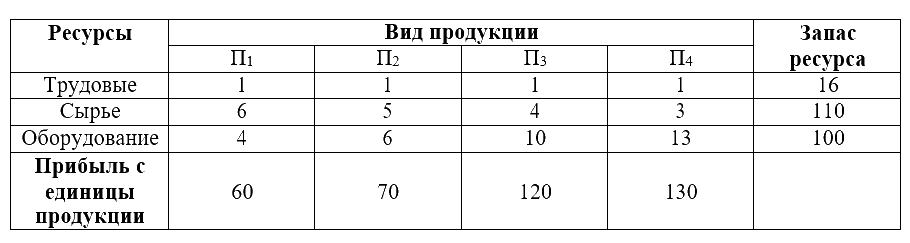
Запишем математическую модель задачи.
Пусть х1, х2, х3, х4 – план выпуска продукции П1, П2, П3, П4 соответственно. Тогда математическая модель задачи выглядит следующим образом:

Решение такой задачи графическим методом невозможно, так как количество переменных равно 4.
Для решения таких задач используется так называемый симплекс-метод.
Для того, чтобы применить симплекс-метод запишем математическую модель задачи в виде:

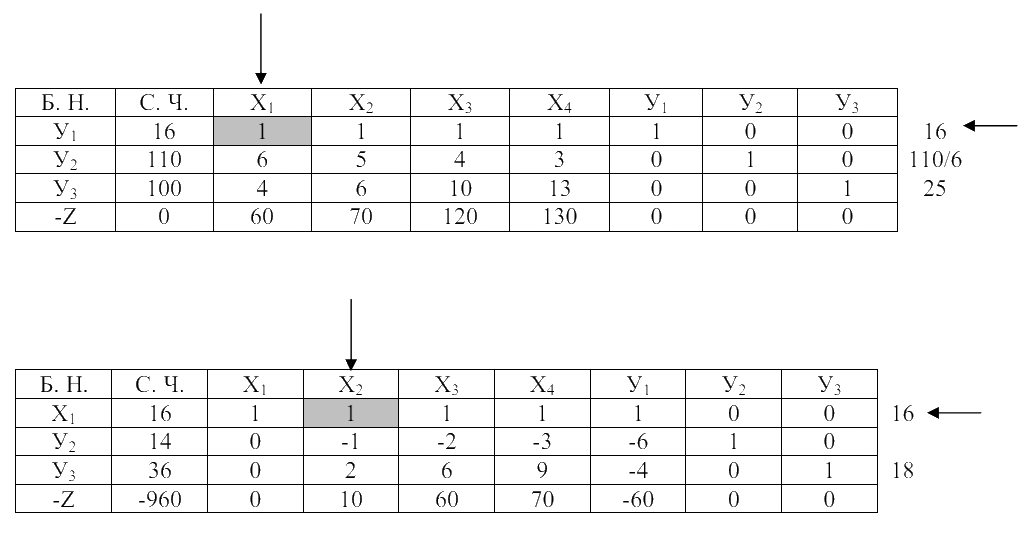

Zmax = 1320. При этом x1 = 10, x2 = 0, x3 = 6, x4 = 0