Раздел 5. Задачи в условиях неопределенности
5.2 Решение задач в условиях риска
Принятие решений в условия риска - это принятие решения в условиях, когда каждая стратегия оперирующей стороны связана с множеством возможных исходов, причем каждый исход имеет определенную вероятность появления, известную исследователю операции.
- При наличии условий риска все рекомендации исследования операции по выбору оптимальной стратегии неизбежно основаны на определенных (статистических) характеристиках случайных факторов. Поэтому, принимая решение о выборе оптимальной стратегии, руководитель всегда рискует в конкретной операции получить не тот результат, на который он ориентируется, исходя из статистических данных.
- Подходы к принятию решений в условиях риска удобно рассматривать на примере некоторой операции, в которой число возможных стратегий и число возможных исходов операций – конечно.
Пусть 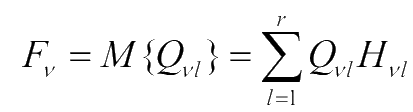 - набор возможных стратегий;
- набор возможных стратегий;
 - набор возможных исходов, причем стратегия
- набор возможных исходов, причем стратегия 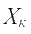 представляет собой одно из значений вектора управления
представляет собой одно из значений вектора управления 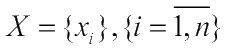 ,
принадлежащее области
,
принадлежащее области  его допустимых значений;
его допустимых значений;
 - значение некоторого показателя эффективности операции в случае появления l -го исхода при реализации оперирующей стороной k -ой стратегии;
- значение некоторого показателя эффективности операции в случае появления l -го исхода при реализации оперирующей стороной k -ой стратегии;
 - вероятность появления l -го исхода при k -ой стратегии.
- вероятность появления l -го исхода при k -ой стратегии.
В стохастической ЗПР эти вероятности предполагаются известными. Итак, подходы к принятию решений в условиях риска удобно представлять в виде таблицы.

Примеры.
- Выполнение плана предприятием при случайном поступлении комплектующих элементов и сырья.
- Доставка грузов в транспортной сети.
- Планирование работ при большом числе операций.
При оптимизации решения в условиях риска широкое распространение получили следующие два принципа:
1) Искусственное сведение к детерминированной задаче.
2) Оптимизация в среднем.
Первый принцип состоит в том, что неопределенная вероятностная картина явления приближенно заменяется детерминированной, т.е. все случайные факторы приближенно заменяются не случайными характеристиками этих факторов, как правило, их математическими ожиданиями. В результате стохастическая ЗПР заменяется детерминированной ЗПР . Этот прием применяется преимущественно в грубых, ориентированных расчетах, а также в тех случаях, когда диапазон возможных значений случайных величин сравнительно мал.
Кроме того, указанный прием применяется и приводит к тому же результату, что и «оптимизация в среднем», в тех случаях, когда показатель эффективности исхода операции зависит от случайных параметров линейно; он получил широкое применение при решении ЗПР с использованием методов сетевого планирования и управления.
Второй принцип (прием) – оптимизация в среднем является более сложным. Он применяется в тех случаях, когда разброс случайных факторов велик и замена некоторых из них их математическими ожиданиями может привести к большим ошибкам.
Рассмотрим прием «оптимизации в среднем».
Пусть Х – вектор управления; А – массив детерминированных факторов  – конкретные реализации случайных факторов;
– конкретные реализации случайных факторов;
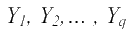 – случайные величины,
– случайные величины,
тогда показатель эффективности является случайной величиной.
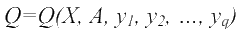
Прием «оптимизация в среднем» состоит в переходе исходного случайного показателя эффективности 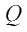 к его некоторой усредненности, статистической характеристике, например к его математическому ожиданию
к его некоторой усредненности, статистической характеристике, например к его математическому ожиданию 

где В - массив известных статистических характеристик случайных величин 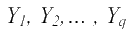 ;
;
 - закон распределения вероятностей случайных величин
- закон распределения вероятностей случайных величин 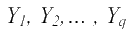 .
.
При оптимизации в среднем по критерию (2) выбирается стратегия, которая, удовлетворяя ограничениям на область  , максимизирует значение F =
, максимизирует значение F =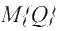 исходного показателя эффективности
исходного показателя эффективности 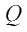 . Оптимальная стратегия должна удовлетворять условию:
. Оптимальная стратегия должна удовлетворять условию:

Такой выбор означает, что в качестве оптимальной стратегии  применяется такая, которая при многократном повторении операции в одинаковых условиях приводит к наилучшему в среднем результату.
применяется такая, которая при многократном повторении операции в одинаковых условиях приводит к наилучшему в среднем результату.
Всякая другая стратегия дает в среднем более плохой результат.
Выбор той или иной статистической характеристики исходного показания эффективности 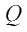 в качестве критерия оптимальности F при «оптимизации в среднем» представляю собой концептуальную проблему, решаемую на уровне руководителя операции.
Рассмотрим процедуру выбора оптимальной «в среднем» стратегии в операции, имеющей дискретный характер, т.е. конечное число возможных стратегий и возможных исходов. В этой операции для каждой k-ой стратегии
в качестве критерия оптимальности F при «оптимизации в среднем» представляю собой концептуальную проблему, решаемую на уровне руководителя операции.
Рассмотрим процедуру выбора оптимальной «в среднем» стратегии в операции, имеющей дискретный характер, т.е. конечное число возможных стратегий и возможных исходов. В этой операции для каждой k-ой стратегии 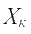 {см. табл. выше} может быть определено математическое ожидание показателя эффективности по формуле:
{см. табл. выше} может быть определено математическое ожидание показателя эффективности по формуле:
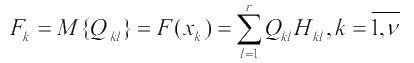
В качестве оптимальной стратегии  при оптимизации «в среднем» выбирается такая стратегия из v возможных стратегий
при оптимизации «в среднем» выбирается такая стратегия из v возможных стратегий  которая удовлетворяет условию:
которая удовлетворяет условию:
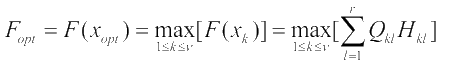
Выражения (4) и (5) по смыслу равнозначны выражениям (2) и (3), т.е. они представляют собой дискретный аналог этих выражений {(2),(3)}.
Таким образом, как видно из выражения (2), прием «оптимизация в среднем» сводит задачу принятия решения в условиях риска к детерминированной постановке.
Действительно, усредненный критерий оптимальности (2) зависит только от стратегий оперирующей стороны и неконтролируемых фиксируемых неслучайных факторов, представленных массивами А и В.
К аналогичному результату приводит и прием «искусственное сведение к детерминированной схеме». Следовательно, все те методы, которые применены для решения ЗПР в детерминированном случае, т.е. с успехом использованы для решения ЗПР в условиях риска, если эта задача с помощью какого-либо приема сведена к детерминированной постановке. Сравнение двух описанных принципов оптимизации стохастических ЗПР показывает, что они представляют собой детерминизацию исходной задачи на разных уровнях влияния стохастических факторов:
- Прием «искусственное сведение к детерминированной схеме» представляет собой детерминизацию на уровне факторов.
- Прием «оптимизация в среднем» представляет собой детерминизацию на уровне показателя эффективности.